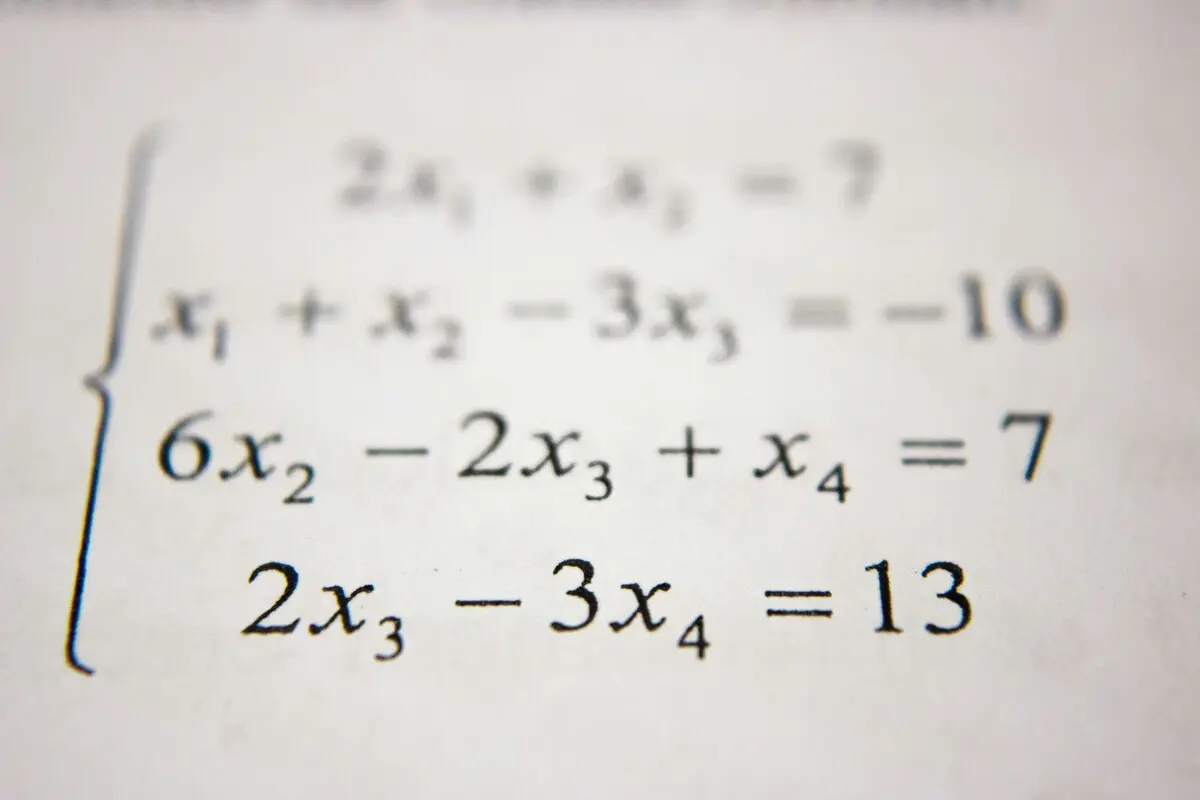Un piano di studi per Matematica Generale.
Modulo 1: Concetti Fondamentali di Algebra
- Insiemi e operazioni fondamentali
- Numeri reali e complessi
- Algebra delle equazioni e disequazioni
- Polinomi e frazioni algebriche
- Sistemi di equazioni lineari e metodo di Gauss
Modulo 2: Funzioni e Limiti
- Concetto di funzione: dominio, codominio e grafico
- Funzioni elementari: potenze, esponenziali, logaritmi e trigonometriche
- Limiti di funzioni e forme indeterminate
- Teoremi sui limiti (Weierstrass, Bolzano, Cauchy)
- Continuità delle funzioni e punti di discontinuità
Modulo 3: Calcolo Differenziale
- Derivate e significato geometrico
- Regole di derivazione (somma, prodotto, quoziente, catena)
- Derivate di funzioni elementari
- Studio di funzione e punti critici
- Teoremi di Rolle e Lagrange
- Approssimazione lineare e differenziale totale
Modulo 4: Calcolo Integrale
- Definizione di integrale indefinito
- Regole di integrazione: per parti, per sostituzione, razionali
- Integrale definito e Teorema fondamentale del calcolo
- Applicazioni degli integrali: aree, volumi e media integrale
- Integrali impropri e criteri di convergenza
Modulo 5: Algebra Lineare e Geometria Analitica
- Spazi vettoriali e basi
- Matrici, determinanti e operazioni fondamentali
- Autovalori e autovettori
- Sistemi lineari e teorema di Rouché-Capelli
- Geometria cartesiana: rette, piani e coniche
Modulo 6: Successioni e Serie
- Definizione e tipi di successioni
- Limite di una successione e criteri di convergenza
- Serie numeriche: definizioni e convergenza
- Serie di potenze e serie di Taylor
- Applicazioni delle serie nello sviluppo di funzioni
Modulo 7: Elementi di Probabilità e Statistica
- Probabilità e variabili aleatorie
- Distribuzioni discrete e continue
- Media, varianza e deviazione standard
- Teorema del limite centrale
- Applicazioni della probabilità in matematica generale